SERIES AC CIRCUITS

In this article, we will study about the various AC series circuit ,how do they functions and its various parameters.

Some common AC series circuits are:

AC RL series circuit - It consists of Resistance & Inductance in series with A.C source.

AC RC series circuit - It consists of Resistance & Capacitance in series with A.C source.

AC RLC series circuit - It consists of Resistance, Inductance & Capacitance in series with A.C source.

We discuss each circuit thoroughly.

RL SERIES CIRCUIT

A RL series circuit having resistance R and inductance L is shown in the figure below.

RL SERIES CIRCUIT

Let, V = RMS value of applied voltage.
       I = RMS value of current
      Vr = Voltage drop across resistance = I*R
      Vₗ = Voltage drop across inductance =  I*Xₗ

We know that current in the pure inductance circuit lags behind the voltage by 90 degree. Therefore, Voltage drop across inductance, Vₗ is ahead of I by 90 degree. 

Phasor diagram of series RL circuit is shown in figure.
* Voltage drop across R is in phase with the current.
* Voltage drop across L leads current by 90.

PHASOR DIAGRAM OF RL SERIES CIRCUIT

*Note that Applied Voltage leads the current in the RL series Circuit .

Applied voltage is phasor sum of the voltage across resistance & voltage across inductance.

V = √{(Vr)² + (Vₗ)²}

V = √{(I*R)² + (I*Xₗ)²}

V = I * √{(R)² + (Xₗ)²}

I = V / √{(R)² + (Xₗ)²}

The quantity √{(R)² + (Xₗ)²} represents impedance,Z of the RL series circuit.

Z = √{(R)² + (Xₗ)²}.

Apparent power -It is the product of the RMS value of applied voltage and RMS value of the current. Its unit is Volt Ampere (VA).

Apparent power = V*I

True power -It is the product of RMS applied voltage and the component of the current in phase with V. Its unit is in Watts (W).

True power = V * (I*cosⲫ)         {I*cosⲫ is component of current in phase with V}

Power factor of RL Series Circuit

Power factor is defined as the cosine of the angle between voltage and current. As seen from  the phasor diagram, current is lagging behind the applied voltage by angle ⲫ.

So from phasor diagram,

Power Factor = cosⲫ = Vr / V.

cosⲫ = I*R / I*√{(R)² + (Xₗ)²}.

cosⲫ = R / √{(R)² + (Xₗ)²}.

cosⲫ = R/Z = Resistance / Impedance.

Hence,
- Power factor = Resistance /  Impedance

- Power factor = True Power / Apparent Power

RC SERIES CIRCUIT

A RL series circuit having resistance R and capacitance C is shown in the figure below.

RC SERIES CIRCUIT

Let, V = RMS value of applied voltage.
       I = RMS value of current
      Vr = Voltage drop across resistance = I*R
      Vc = Voltage drop across capacitance =  I*Xc

We know that current in the pure capacitance current leads the voltage by 90 degree. Therefore,current I is 90 degree ahead of Voltage drop across capacitance, Vc.

Phasor diagram of series RC circuit is shown in figure. 

* Voltage drop across R is in phase with the current 
* Voltage drop across C lags behind current by 90.

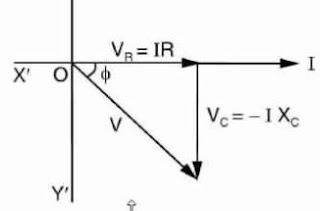PHASOR DIAGRAM OF RC SERIES CIRCUIT

*Note that current leads the applied voltage in RC Series Circuit.

Applied voltage is phasor sum of the voltage across resistance & voltage across inductance.

V = √{(Vr)² + (Vc)²}

V = √{(I*R)² + (I*Xc)²}

V = I * √{(R)² + (Xc)²}

I = V / √{(R)² + (Xc)²}

The quantity √{(R)² + (Xc)²} represents impedance,Z of the RC series circuit.

Z = √{(R)² + (Xc)²}.

Power factor of RC Series Circuit

Power factor is defined as the cosine of the angle between voltage and current. As seen from  the phasor diagram, applied voltage is lagging behind the current by angle ⲫ.

So from phasor diagram,

Power Factor = cosⲫ = Vr / V.

cosⲫ = I*R / I*√{(R)² + (Xc)²}.

cosⲫ = R / √{(R)² + (Xc)²}.

cosⲫ = R/Z = Resistance / Impedance.

Hence,
- Power factor = Resistance /  Impedance

- Power factor = True Power / Apparent Power

RLC SERIES CIRCUIT

A RLC series circuit having resistance R , inductance L and capacitance C is shown in the figure below.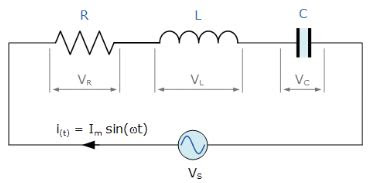

RLC SERIES CIRCUIT

Let, V = RMS value of applied voltage.
       I = RMS value of current
      Vr = Voltage drop across resistance = I*R
      Vₗ = Voltage across inductance = I*X
      Vc = Voltage drop across capacitance =  I*Xc



Phasor diagram of series RLC circuit is shown in figure. 

* Voltage drop across R is in phase with the current. 
* Voltage drop across L leads the current by 90 degree.
* Voltage drop across C lags behind current by 90 degree.

PHASOR DIAGRAM OF RLC SERIES CIRCUIT

As seen from the phasor diagram that Vₗ and Vc are 180 degree out of phase, they are direct opposite to each other. So effective voltage will be (Vₗ-Vc).

Applied voltage is phasor sum of the voltage across resistance & effective voltage.

V = √{(Vr)² + (Vₗ -Vc)²}

V = √{(I*R)² + (I*Xₗ - I*Xc)²}

V = I * √{(R)² + (Xₗ - Xc)²}

I = V / √{(R)² + (Xₗ- Xc)²}

The quantity √{(R)² + (Xₗ - Xc)²} represents impedance,Z of the RLC series circuit.

Z = √{(R)² + (Xₗ - Xc)²}.

Power factor of RLC Series Circuit

Power factor is defined as the cosine of the angle between voltage and current. As seen from  the phasor diagram, applied voltage is lagging behind the current by angle ⲫ.

So from phasor diagram,

Power Factor = cosⲫ = Vr / V.

cosⲫ = I*R / I*√{(R)² + (Xₗ - Xc)²}.

cosⲫ = R / √{(R)² + (Xₗ - Xc)²}.

cosⲫ = R/Z = Resistance / Impedance.

Hence,
- Power factor = Resistance /  Impedance

- Power factor = True Power / Apparent Power

If Xc > Xₗ , then current leads the voltage.

If Xc < Xₗ , then current lags behind the voltage.

If Xc = Xₗ , then current is in phase with voltage and power factor is unity.

Thanks for reading.
Keep Sharing & loving.